Z-Transform

Main Source:

• Various source from Google and YouTube

Z-transform is the discrete version of Laplace transform, often used in the digital world.

Z-transform is defined as follows:

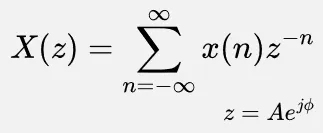
• $x(n)$: the n-th term of the sample
• $z$: complex variable
• $A$: magnitude
• $j$: imaginary unit
• $\phi$: phase angle in radian.

Discrete sum $\sum$ is used instead of continuous integration. The sum goes from negative infinity to positive infinity, which is not possible in the real world. Typically, only some number of sample is used, as long as the number of sample is sufficiently large, so it doesn't affect the accuracy of the Z-transform.

How does it work

Z-transform is just the discrete version of Laplace transform, the way of how it works is similar as the discrete Fourier transform to Fourier transform. By multiplying each discrete sample by the complex variable $z^{-n}$, we are essentially converting the sample from the time domain to the frequency domain by shifting the sample to a different frequency. The shifts depend on the power of $n$ that vary between samples.