Discrete Fourier Transform

Main Source:

• Various source from Google and YouTube

Discrete Fourier transform (DFT) is the discrete signal version of the Fourier transform. DFT is widely used in digital signal processing because computers can only process discrete signals. One application of DFT is removing noises or filtering specific frequencies from digital signal.

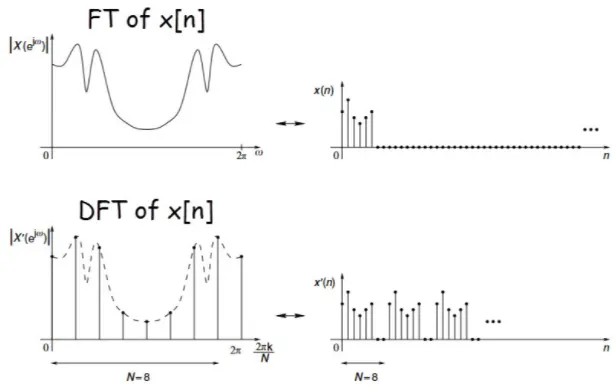
Source: https://www.ee-diary.com/2023/05/what-is-discrete-fourier-transformdft.html#

How does it work

The formula for DFT is:

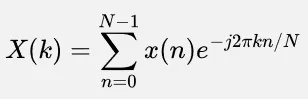
• $n$: Sample index
• $N$: Number of samples
• $k$: Frequency bin index
• $X(k)$: The k-th frequency component of the signal
• $x(n)$: The n-th sample of the input sequence
• $j$: The imaginary unit
• $e^{-j2 \pi k n / N}$: The exponential term involving $2\pi k n /N$ to convert frequency from cycles per second to radians per sample.

A discrete signal is made by sampling a continuous signal. The sampling process takes a sequence of equally spaced point of the continuous signal. The number of sample is called $N$ and the number of samples must be an integer power of 2.

In FT, we multiply the exponential term (representation of sine and cosine waves) with $f(t)$, the signal function. While in DFT, the signal function is replaced by the n-th sample $x(n)$, which increase up to the number of sample $N$. The sample is represented as complex-number vector.

The resulting product is a complex number that represents the contribution of that specific sample to the k-th frequency component of the signal in the frequency domain. It has a magnitude and a phase angle that depend on the value of the sample $x(n)$ and the frequency bin index $k$.

Computation

FT is a continuous-time transform that involves integration over an infinite time interval. Its computation is typically performed using numerical integration techniques. FT can be computationally expensive for large bandwidth or a complex frequency structure.

In DFT, with input signal and the exponential term being represented in vector, the multiplication between them result in a matrix multiplication. With a straightforward algorithm, DFT can be computed in $O(N^2)$ time, where $N$ is the number of samples in the signal.

Next topic is an improvement for DFT algorithm which is the Fast Fourier transform (FFT) algorithm.