Wavelets
Main Source:
Fourier transform represent signal in sinusoidal function. Sometimes, this is not suitable for signals that has abrupt changes. For example, sine wave is periodic, which means it will repeat at some point. If a signal changes abruptly, like sudden jumps or discontinuities, the Fourier Transform may struggle to accurately represent these features.
Wavelet is a short periodic function, meaning that the function doesn't oscillate forever unlike sinusoidal function. This characteristic make wavelets localized, which means that the same function can have various shape to match different regions of a signal. Wavelets can adapt their shape and size, capturing localized information at different scales.
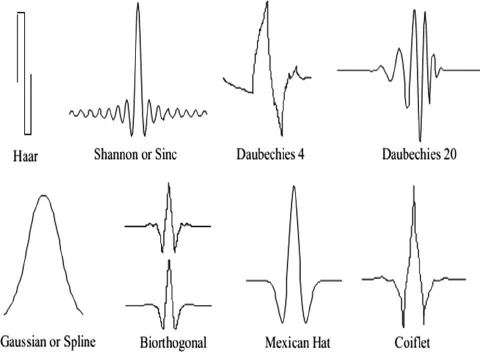
Wavelets Operations
These are some examples of common and general purpose wavelets function (also called mother wavelet or basis function). They serve as prototype, from which other wavelets and localized shape are derived through stretching (scaling) and translation (shifting).
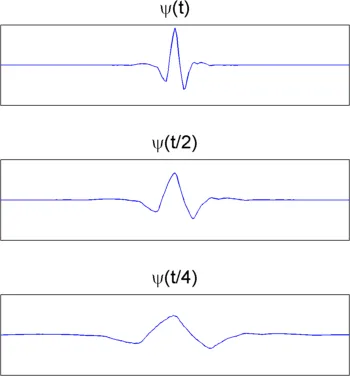
Source: https://www.mathworks.com/help/wavelet/gs/continuous-wavelet-transform-and-scale-based-analysis.html
A scaling operation of wave function to a scale of 1/2 and 1/4.
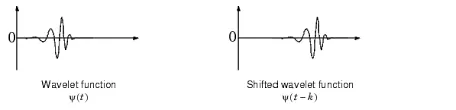
Source: https://inst.eecs.berkeley.edu/~ee225b/sp14/lectures/wavelets-g&w.pdf
A shifting operation by .
Wavelet basis functions are multiplied by the original signal to obtain wavelet coefficients. Similar to the Fourier transform, this process effectively measures the contribution of each wavelet to the signal. We can efficiently represent signals using these wavelet coefficients. These coefficients can now be used to filter noise, compression, or etc. by discarding specific frequency of the signal.