Diffie-Hellman

Main Source:

• Diffie–Hellman key exchange — Wikipedia

Diffie-Hellman Key Exchange is a cryptographic protocol to securely exchange a secret key over a public communication. It was one of the earliest example of public-key cryptography or asymmetric cryptography.

Explanation

The Diffie-Hellman key exchange is based on mathematical concepts including the modular exponentiation and the difficulty of the discrete logarithm problem. The protocol relies on mathematical operations performed in a finite field.

1. Public Key Agreement: Each party, often denoted as Alice and Bob, agree on two number: $p$, which is a prime number and $g$, which is the base value.
2. Key Generation: Both parties choose their own private key (an integer), let's say Alice's private key is $a$ and Bob's private key is $b$.
3. Public Key Calculation: Alice's public key (denoted as $A$) is obtained by $A = g^{a} \text{ mod } p$, and for Bob (denoted as $B$) is similar: $B = g^{b} \text{ mod } p$. After the calculation, they will share the public key to each other.
4. Compute Secret Key: The shared secret key, denoted as $s$ is computed as follows: For Alice, $s = B^a \text{ mod } p$. Similarly, for Bob, $s = A^b \text{ mod } p$.

That's it, they will have the same secret key. The secret key is not shared in public, they will derive the secret key on their own. Although they chose a different number (their own private key), they will still arrive at the same secret key.

The most important math properties of why this works is described as the following formula:

$(g^a \text{ mod } p)^b \text{ mod } p = (g^b \text{ mod } p)^a \text{ mod } p$
or
$A^b \text{ mod } p = B^a \text{ mod } p$

This equation demonstrates that if Party A raises the result of $g^a \text{ mod } p$ to the power of $b$ and takes the modulus $p$, it will yield the same result as Party B raising the result of $g^b \text{ mod } p$ to the power of $a$ and taking the modulus $p$. This property allows both parties to compute the same shared secret key without directly exchanging their private keys.

Source: https://www.pcmag.com/encyclopedia/term/diffie-hellman

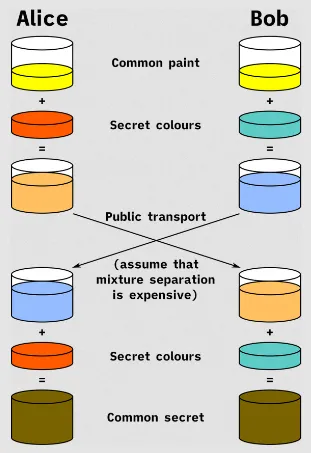
Here is an analogy of Diffie-Hellman key exchange in terms color combination.

Source: https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange#/media/File:Diffie-Hellman_Key_Exchange.svg

Security

If an attacker were to brute force the secret key, the attacker would need to compute the secret key formula, which is $(g^a \text{ mod } p)^b \text{ mod } p$ or $(g^b \text{ mod } p)^a \text{ mod } p$. Note that only $a$ and $b$ are kept secret, all the other values such as $p$, $g$, $g^a \text{ mod } p$, and $g^b \text{ mod } p$ are sent in clear.

The hacker would need to solve for $g^{ab} \text{ mod } p = g^{ba} \text{ mod } p$, which is equal to the secret key formula. As $a$, $b$, $p$ grow larger, the complexity grows exponentially, making it computationally infeasible for large values. Therefore, it is crucial to select larger values to ensure the security of the Diffie-Hellman key exchange.