Skip to main content

Traversal

Main Source:

Traversal refers to the process of visiting and accessing each element or node in a data structure, such as linked list, tree, or graph. The purpose of traversal is to perform some operation on each element or node, such as reading its value, modifying it, or performing other specific task.

For a singly linked list, traversal involves starting at the head node and following the links from one node to the next until the end of the list is reached. This is typically done using a loop or recursion.

Graph Traversal​

Graph traversal refers to the process of exploring nodes or vertices in a graph data structure. There are two commonly used methods for graph traversal: depth-first search (DFS) and breadth-first search (BFS).

Depth-First Search (DFS)​

DFS is a graph traversal algorithm that explores vertices as deeply as possible. It starts at a given vertex, visits one of its neighbors, and continues to explore that neighbor's neighbors until it reaches a dead end. After reaching dead end, it will come back to the previous vertex and continue to visit that vertex neighbor until it reaches a dead end again.

Here is the pseudocode:

DFS(graph, vertex, visited):
    visited add vertex                              // mark as visited
    process(vertex)                                 // process it as needed

    for neighbor in the neighbors of graph(vertex): // visit each of the neighbor
        if neighbor is not in visited:              // only visit the unvisited
            DFS(graph, neighbor, visited)           // recursive call

In DFS, we will visit a vertex as deep as possible, each vertex have a neighbor, and that neighbor will have another vertex. After reaching dead end, we will continue exploring the neighbors of the previous vertex. This behavior aligns closely with stack and recursion, therefore we can use recursion and take advantage of its call stack to implement DFS.

It is possible that the graph we are traversing consists of a loop (cyclic graph). If we keep traversing it mindlessly, we may never finish our recursion function, which will result in stack overflow error. To mitigate this, we will have another data structure called visited, which will keep track the visited vertex. We will only traverse to unvisited vertex. The data structure of visited can be a set data structure, to ensure fast retrieval of element and to store only unique element.

DFS GIF
Source: https://en.m.wikipedia.org/wiki/File:Depth-First-Search.gif

Breadth-First Search (BFS)​

BFS, also called level-order search, is a graph traversal algorithm that explores all vertices of a graph at the same level before moving to the next level. It starts at a given vertex and explores all its neighboring vertices before moving on to their neighbors.

BFS(graph, start):
    visited = set()                // Keep track of visited vertices
    queue = Queue()                // Initialize an empty queue
    queue.enqueue(start)           // Enqueue the starting vertex

    while queue is not empty:
        vertex = queue.dequeue()   // Dequeue a vertex from the front of the queue

        if vertex is not in visited:
            visited.add(vertex)    // Mark the vertex as visited
            process(vertex)        // Process the vertex as needed

            // Enqueue unvisited neighbors
            for neighbor in graph.adjacentVertices(vertex):
                if neighbor is not in visited:
                    queue.enqueue(neighbor)

BFS doesn't use recursion to traverse, it instead uses a queue data structure to keep track all the neighbors in the current level.

The algorithm starts by enqueuing the starting vertex into the queue and marking it as visited. It then enters a loop where it repeatedly dequeues a vertex from the front of the queue, marks it as visited, process it depending on the task, and enqueues its unvisited neighbors. This process continues until the queue becomes empty, indicating that all vertices have been visited.

tip

The queue act like a "to-do list" to keep track all the node for us to visit later.

BFS GIF
Source: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif

Tree Traversal​

As we know, a tree data structure is a special case of graph where it is undirected and acyclic. We can also use DFS and BFS to traverse a tree (the previous GIF is literally a graph organized tree structure).

Both BFS and DFS are a general graph traversal algorithm that can be applied on arbitrary graph and tree. Depending on the structure, the algorithm should be similar.

In tree traversal using DFS, there are specific orders of visiting and processing the nodes in a tree, which are inorder, preorder, and postorder. Let's assume we are traversing a binary tree.

Inorder Traversal​

In inorder traversal of a binary tree, we will visit the left subtree, then the current node, and finally the right subtree. By visiting the left subtree, it means we are going to visit all the child in the left subtree in recursive manner (DFS).

function DFS(node):
    if node is not null:
        DFS(node.left)
        visit(node)
        DFS(node.right)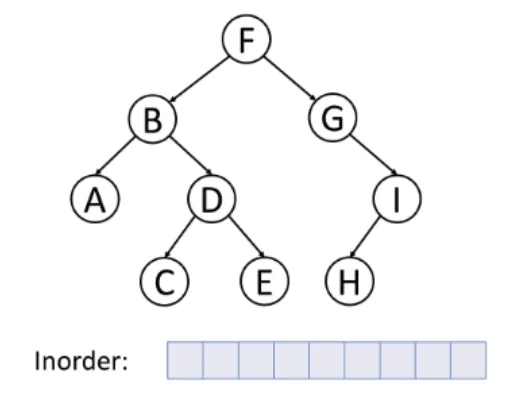

Inorder traversal
Source: https://commons.wikimedia.org/wiki/File:Inorder-traversal.gif (red means all the child has been visited)

Preorder Traversal​

In preorder traversal, we visit the current node first, then the left subtree, and finally the right subtree.

function DFS(node):
    if node is not null:
        visit(node)
        DFS(node.left)
        DFS(node.right)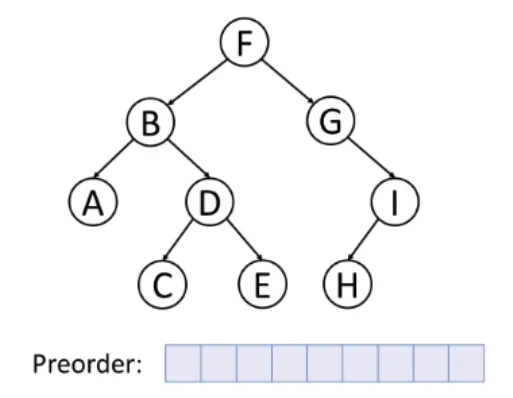

Preorder traversal
Source: https://commons.wikimedia.org/wiki/File:Preorder-traversal.gif

Postorder Traversal​

In postorder traversal, we visit the left subtree first, then the right subtree, and finally the current node.

function DFS(node):
    if node is not null:
        DFS(node.left)
        DFS(node.right)
        visit(node)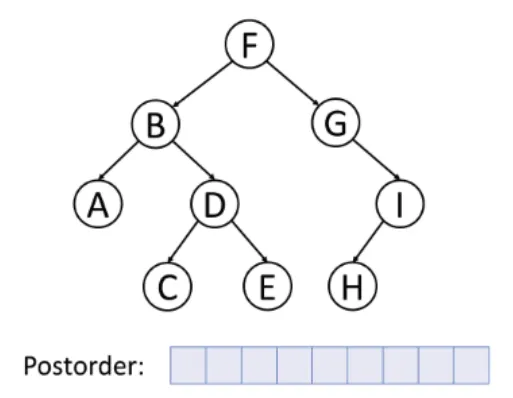

Postorder traversal
Source: https://commons.wikimedia.org/wiki/File:Postorder-traversal.gif

Depending on the task, the order of visiting nodes matters. For example, inorder traversal can be used to visits the nodes in ascending order in the case of a binary search tree.