Search

Main Source:

• Data Structures & Algorithms — Computer & Programming Fundamentals (with some rephrasing)

Search algorithms are algorithm that is used to locate a specific item or element within a collection of data. The collection of data can take various forms, such as an array, list, tree, graph, or any other data structure.

This note explains the simple linear and binary search algorithm, other search algorithm for more complex data structure are explained in the other notes. (e.g., searching in tree with DFS).

Linear Search

Linear search, also known as sequential search, is the simple and intuitive search algorithm that sequentially checks each element in a collection of data until a match is found or the entire collection has been traversed. It is applicable to both sorted and unsorted data.

function linearSearch(array, target):
    for i from 0 to length(array) - 1 do:
        if array[i] equals target then:
            return i  // Return the index where the target is found
        end if
    end for

    return -1  // Return -1 if the target is not found
end function

Linear search iterates from the beginning of the array/list, then check each element if it is the element we are looking for. If so, we will return the element and complete the search, else continue with the iteration. If we don't find the target element, we typically return -1 to indicate the target is not found.

Linear search results in best $O(1)$ time, when the target element is at the beginning, average of $O(n)$ time, and the worst-case scenario in $O(n)$ time, which occurs when the target element is at the end of the collection. Linear search does nothing other than checking if the element in the array is equal to the target, it requires constant extra memory.

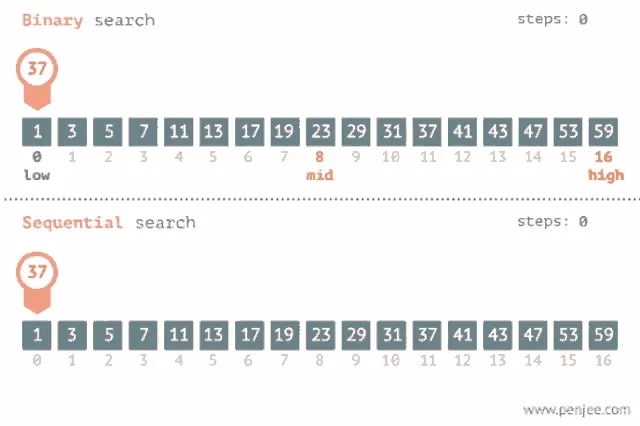
Binary Search

Binary search is a searching algorithm, used for searching an element in a sorted collection.

Binary search assumes that the collection is in sorted order, the idea is that, we don't need to look for the target element in the range of elements where they are smaller than the target element. Binary search will simply eliminate the portion of element that we think doesn't make sense to look in for.

function binarySearch(array, target):
    low:= 0
    high:= length(array) - 1

    while low <= high do:
        mid:= (low + high) / 2
        if array[mid] equals target then:
            return mid  // Return the index where the target is found
        else if array[mid] < target then:
            low:= mid + 1
        else:
            high:= mid - 1

    return -1  // Return -1 if the target is not found
end function

Binary search starts checking in the middle, it checks if the element in the middle is larger or smaller than the target element. If it is smaller, then it will be impossible for our target element to be present in the smaller element range. We will eliminate that portion and search the other range of elements. This will effectively divide the search space by half until the target is found, or the target does not exist in the collection.

Binary search efficiently reduces the search space by half in each iteration, resulting in a logarithmic $O(\log n)$ time complexity, where $n$ is the number of elements in the sorted array. It is significantly faster than linear search for large datasets. However, it requires a sorted collection, sorting an unsorted collection first would result longer than linear search, since a typical sorting algorithm requires $O(n \log n)$ time.

Similar to linear search, binary search require constant memory space. No matter how large the collection is, the low, mid, and high pointer will always store an integer index.

Source: https://tenor.com/view/binary-search-sequence-search-gif-20595028