Skip to main content

Data Types

Main Source:

  • Book 2 chapter 7

Data type is a classification or categorization of data that determines the type of values that a variable can hold, the operations that can be performed on those values, and the way the values are represented in memory.

Type Systems​

Type system is a set of rules, constraints, and mechanisms in programming languages that define and enforce the types of values and expressions used in a program. It consists of:

  • Built-in types (also called primitive or predefined types), common types include boolean, integer, char, float, double, etc. These are typically supported in hardware.
  • Mechanism to declare and define new types.
  • Rules for type equivalence, how to decide if one name is the same type of another name.
  • Type compatibility, what operation can be performed on some types.
  • Type conversion, a way to convert one type to another, explicitly or implicitly.
  • Type inference, an optional feature to automatically deduces the types of expressions and variables without explicit type annotations.

With a type system, compilers determine the appropriate operation to perform on operands. For example, if a and b are integers, then a + b will result in an integer addition. If b is a floating-point number, the compiler checks whether addition between an integer and a floating-point number is allowed or defined by the user. If both answers are negative, the compiler may choose to throw an error or implicitly convert one type to another.

Some term about type system:

  • Strong typing vs weak typing: A strongly typed language will never convert one type to another when the operation between them are not supported. Weak typed language may perform this if needed, which can potentially lead to unexpected errors.
  • Static typing vs dynamic typing: A statically typed language does type checking at compile-time, which results in variable must be annotated by its type (expect if it has type inference) when declared. Dynamic typed is the opposite, it does type checking at runtime, and variable doesn't require explicit type annotation. By checking the type at runtime, a variable can hold different type of values during the execution of the program.

Polymorphism​

Polymorphism allows for entities (variables, functions, etc.) to have multiple types or behave differently depending on the types of their arguments.

While polymorphism depends on type it operates on, it doesn't always imply type checking is done at runtime.

  • A straightforward ad-hoc polymorphism like function/method overloading, in which multiple functions have the same name, but has different argument(s) or type of the argument(s). Compiler can distinguish between them by comparing the number of parameters or type of the parameters.
  • Subtype polymorphism allows a subtype to be used where a supertype is expected. This may be encountered in OOP languages, where exists concept like inheritance that allows objects of different classes or types to be treated uniformly through common interfaces or base classes.
  • A situation where single function or data structure can operate on values of different types, this is called parametric polymorphism. It may be explicit (often known as generics), where programmer specifies the function that can work on some types and another; or implicit (often known as type inference), where the compiler infer the type parameters it works on.

Classification of Types​

  • Numeric Types: Represent numerical values. They include integer types (such as int, long, short) for representing whole numbers, floating-point types (such as float, double) for representing decimal numbers, and sometimes additional types like byte, decimal, complex numbers.

  • Enumeration Types: Enumeration types define a set of named values. They represent a finite set of distinct options or choices. Each value in an enumeration type is typically assigned an integer (called ordinal value) as an underlying representation. Enums provide a way to express a set of related constants and make the code more readable and expressive.

    For example, enum in C++:

    enum class Color { RED, GREEN, BLUE };
    Color myColor = Color::GREEN;

    // Using the enum values
    if (myColor == Color::RED)
        // ...

    Under the hood, integer comparison are going on.

  • Subranges Types: Subrange types allow to define a subset of values within a range of values. For example, a subrange type Age may restrict values to be within a specific range, like 0 to 120. Pascal language is first to implement subrange type, for example, we can define: type test_score = 0..100;, restricting it to only be defined under the range of 0 to 100.

  • Composite Types: Composite types are types that are composed of multiple values or subtypes. They are created with type constructor and used to represent structured or compound data. Examples of composite are arrays, lists, tuples, records, structs, classes, and objects. Composite types allow grouping related data together, making it easier to organize.

Orthogonality​

Orthogonality is a characteristic of an entity having independent and non-overlapping features or dimensions. An orthogonal type system has independent type features that can be combined in many ways without restrictions or conflicts. In other word, changing feature A doesn't affect feature B. To achieve orthogonality, types need to be well-defined and clear meaning, without being ambiguous with others.

For example, a language can support variable being mutable or immutable and nullable or non-nullable.

mutable x: Int; // mutable variable, non-nullable
immutable x: Int; // mutable variable, non-nullable
mutable x?: Int; // mutable variable, nullable
immutable x?: Int; // mutable variable, nullable

We can say immutability is the orthogonal features of this language and the nullable types as the orthogonal feature of the type system.

Type Checking​

Type checking involves verifying that the types of operands in an operation or expression are compatible, converting between them if necessary, and determining a possibly new type after the operation.

Type Equivalence​

Two types are considered equivalent according to structural equivalence and name equivalence.

  • Structural Equivalence: Structural equivalence compares the structure of two types to determine if they have the same composition of fields, methods, and properties. It looks at the internal structure of types, disregarding their names or declarations.

    The compiler compares their order of declaration, formatting, and evaluate any expression.

    // All these three are same.
    struct Person {
        int age;
        string name;
    };

    struct Person {
        string name;
        int age;
    };

    struct Person { int age; string name; };

    Another example is the subrange type: type test_score = 0..100; should be same as type test_score = 0..10*10; (10 times 10), but different with type test_score = 0..99;.

  • Name Equivalence: Name equivalence compares types based on their names or declarations. It assumes that programmer that writes two types definition treat these types differently. If two types have the same name, they are considered equivalent regardless of their internal structure.

    A language is said to have strict name equivalence if aliased types are considered distinct from each other, otherwise, if they are considered equivalent, it is said to have loose name equivalence.

tip

Aliased types or type aliases allow programmer to create alternative names or aliases for existing types. We can define type alias like using age = int in C++. This defines a new type age that can be used just like a normal type, but it is actually just an int.

Type Conversion​

Type conversion involves changing the type of a value from one data type to another, it can be done explicitly by the programmer (also called type cast), or implicitly by the compiler (also called type coercion).

There are three case in conversion:

  1. In languages that use name equivalence, two types are considered the same if they have the same name, regardless of their structural differences. This means that if two types have different names but are structurally equivalent, they are considered interchangeable in terms of type conversions, because they have the same representation under the hood.
  2. A potentially unsafe type checking that occurs during runtime, that is when two types are different, but they can be represented as other depending on the actual value in runtime. For example, two subrange types are different, but one subrange is just subrange of another.
  3. Types have different low-level representation, but we can define conversion between them.

For example, integer (typically 4 bytes) is a whole number, while double type (typically 8 bytes) is an IEEE floating-point representation with 15 decimal points of precision.

If that integer were to be converted into double, then this would be no problem because double is essentially more precise than an integer. It would be only converting it into larger data types by adding more bit. This is also called type promotion or widening conversion. Type promotion is typically performed implicitly by the programming language without requiring explicit syntax or cast operators.

On the other hand, a double conversion into integer is called type demotion or narrowing conversion. Type demotion can result in potential data loss or truncation, as the value may not fit within the smaller type's range or precision. Therefore, type demotion usually requires explicit casting or conversion operations to indicate that the programmer is aware of the potential loss of information.

For example, converting an integer to a double is "as simple as adding .0" to the number (i.e., 5 becomes 5.0). Conversely, converting a double to an integer involves removing the decimal point (i.e., 5.3 becomes 5), which results in losing some information.

Type Compatibility​

Type doesn't have to be same to be operated together. In other word, both operands must be at least compatible. The compatibility between types can be defined by the language or sometimes by the user. When it is defined by the language, the compiler can implicitly do the type conversion, this is known as type coercion.

Some coercion can be helpful or even lead to an unexpected behavior. For example, it may make sense to allow addition of a string with an integer, this will append the integer to the string. For example, "a string" + 1 = "a string1".

info

In type coercion, the compiler typically prioritizes one conversion over another. For example, in an addition between an integer and a double, the compiler would convert the integer to a double instead of the opposite, in order to avoid information loss.

Other coercion are:

  • Integer to boolean: 0 is false, anything not 0 is true (C language)
  • Truthy and falsy values: In Python, values such as non-zero numeric values, non-empty sequences (e.g., strings, lists, tuples), non-empty containers (e.g., dictionaries, sets) are considered as True.

We can define our own coercion by overloading operators or overloading the conversion itself. In C++:

class MyInt {
private:
    int value;
public:
    MyInt(int val): value(val) {}

    operator int() const {
        return value;
    }

    MyInt operator+(const MyInt& other) const {
        return MyInt(value + other.value);
    }
};

int main() {
    MyInt myInt(42);
    int regularInt = myInt;  // Implicit conversion using the conversion operator
    // regularInt now holds the value of myInt

    return 0;
}

MyInt simply holds an int, but it cannot be coerced or operated with a normal int. To enable such operations, we overload the conversion operator to convert MyInt to an integer using operator int() (called automatically by the compiler), and we also overload the + operator to perform addition between two MyInt objects. Additionally, we can define other operations between a MyInt object and a regular integer or even other types.

Type Inference​

Some expressions are straightforward to deduce the resulting type. Arithmetic operation typically yield the same type as the operands, comparison typically produces boolean, and assignment can be inferred based on the expression being assigned to it. For example, if right-hand side assignment is addition of integer and double, resulting type will be double (assuming integer is converted into double).

Structs & Unions​

Structs (also known as records) are used to define custom data types that encapsulate related data fields or members. A union is a special data type that allows different data types to be stored in the same memory location. This mean, union allocate memory that is shared among all its members. As a result, only one member of the union can be stored and accessed at a time. The union will accommodate size for the largest member within the union.

As seen before, the syntax of declaring a named struct (or union with union keyword instead of struct) in C++ is like:

struct StructName {
    type1 member1;
    type2 member2;
    // ...
    typeN memberN;
};

In memory, struct will be stored in memory layout like below.

Struct in memory
Source: https://nerdyelectronics.com/memory-layout-of-a-structure/

This is an array of room structs, each containing 2 ints and 2 floats, with each element having a size of 4 bytes. The fields of struct are stored next to each other in memory. Some structs may have larger size than they should be, due to data alignment with padding.

Memory allocation of struct and union:

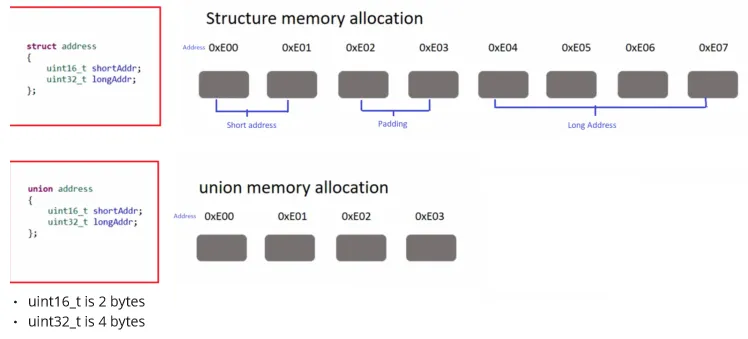
Struct vs union memory allocation
Source: https://fastbitlab.com/microcontroller-embedded-c-programming-lecture-157-unions/ (with modification)

Arrays​

tip

Array as a data structure is explained here.

The syntax of arrays varies between languages. Some languages may require an explicit number for the size of the array, use parentheses instead of square brackets to access elements, and start indexing from 1 instead of 0.

In C language, array is declared in the following syntax dataType arrayName[Size] = {element1, element2, ..., elementN};. For example, an array of integers is declared by int arr[5] = {1, 2, 3, 4, 5};. Then, to access it, we can call the name of array with square bracket and put the index of element we want to access inside it. Accessing element of index 3 is arr[3].

In C++, [] is treated as an operator. Calling arr[3] is a shorthand for arr.operator[](3). Like other operators in C++, they are considered as functions. This makes it possible to overload them, meaning we can use [] to access something from any objects of our classes. Overloading operator[] can be a good way to create an intuitive way of accessing elements from our own custom data structure.

Allocation​

If array size is known at compile-time, then it is easy to allocate memory for it. Sometimes, people specify size of array based on something only known at runtime. For example, declaring an array with the same size of some input integer. Size is indeed specified, but it is based on some runtime input.

There are five cases of allocating an array:

  1. Global Lifetime, Static Shape: When array is created in the global scope, it will exist throughout the entire program's execution. The dimension or the shape of the array (i.e., the size), is known (specified in declaration) and fixed at compile time. Memory for the array is allocated in the static memory.

  2. Local Lifetime, Static Shape: The size of array is specified in the declaration, but it is declared within a function or a block and has a local scope. Memory for the array is allocated on the stack frame during runtime.

  3. Local Lifetime, Shape Bound at Runtime: The array is declared within a function or a block, but the size is not known until runtime. Memory is allocated within the stack frame, but the allocation is hybrid. Stack frame is divided into fixed-size part, to place object whose size is known, and the variable-size part contains object whose size depends on runtime. An example in Python would be: def my_function(): my_array = [0] * n.

  4. Arbitrary Lifetime, Shape Bound at Runtime: The array's lifetime is not strictly tied to a specific scope or function. This is the case when creating an array is just making some reference. We can choose to bound the reference at any time. Languages like Java and C#, which use reference types, rely on this. Declaring an array like int[] A creates a reference; only if we assign it, like A = new int[5];, will the array then be allocated.

  5. Arbitrary Lifetime, Dynamic Shape: In this case, the array's shape can change dynamically during its lifetime. Memory for the array is allocated on the heap, and the size can be adjusted as needed by resizing or reallocating the memory.

    An example in Java would be using an ArrayList.

    ArrayList<Integer> dynamicList = new ArrayList<>();
    dynamicList.add(5);

Memory Layout​

Elements of array are placed contiguously in memory (see also array in memory). The name we use for array is essentially just a pointer that points to the address of first element of the array in memory.

In a multidimensional array, the placement can either be row-major or column-major.

  • In a row-major order, the elements of each row are stored consecutively in memory, and the rows themselves are stored one after another. This means that the elements of the second dimension are stored after the first, and so on.
  • In a column-major order, the elements of each column are stored consecutively in memory, and the columns themselves are stored one after another.

With this array:

arr = [[1, 2, 3, 4],
       [5, 6, 7, 8],
       [9, 10, 11, 12]]

Row-major is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12].
Column-major is [1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12].

Strings​

String is implemented as an array of character. See string as an array.

Sets​

See set data structure.

Pointers & Recursive Types​

Pointers hold memory addresses. It allows for indirect access of an element through its address by dereferencing it. Pointers are commonly used to dynamically allocate memory on the heap. Programming languages that offer manual memory management (e.g., C++) provide the power of pointer, but often introduce memory issues like dangling pointers and memory leaks. Some languages provide tools like garbage collection to automatically manage dynamic allocated memory.

tip

See also pointer & reference.

Recursive types like struct may consist of fields whose type is itself. This is common in data structures like linked list. These types have an unknown size since they may consist of another type, which in turn consists of another type, and so on. For this purpose, we will need to allocate them in memory whose size can change dynamically.

For example, we can create a linked list in C++ like below.

class Node {
public:
    int m_data;
    Node* next;

    Node(int data) {
        m_data = data;
        next = nullptr;
    }
};

int main() {
    Node* head = new Node(1);
    Node* second = new Node(2);
    Node* third = new Node(3);

    // (*head).next = second;
    // (*second).next = second;
    // or simply
    head->next = second;
    second->next = third;

    // Clean up memory
    delete head;
    delete second;
    delete third;

    return 0;
}

When creating linked list, we can use dynamic allocation using the new keyword. The new keyword returns a pointer for the newly allocated memory on the heap.

We created three linked list nodes, and link them together by assigning the appropriate next pointers. head, second, third are all pointer, so we will need to dereference them to actually access the element it contains. It is done by using asterisk in front of the pointer. After dereferencing it, we can access the next field and assign it to appropriate next node. C and C++ provide a way to shorthand the dereferencing and field access. The ptr->field is a shorthand for (*ptr).field.

Lastly, use delete keyword after we have finished using it to deallocate the previously allocated memory. After deleting it, we shouldn't use the pointer anymore. Otherwise, it will cause a dangling reference problem.

tip

Pointer and array are closely linked in C/C++. See these two notes.

Lists​

List is by concept, a data structure that stores a collection of elements in a specific order. List in programming language can be implemented in many ways. One typical implementation is through linked list, array, or dynamic array.