Formal Grammar

Main Source:

• Book chapter 2.1
• Neso Academy playlist 63-64

Formal Grammar is the formalization of grammar, which is the rules to describe languages.

Chomsky Hierarchy

There are many types of formal grammar, the types of grammar based on Noam Chomsky are regular grammar, context-free grammar, context-sensitive grammar, and unrestricted grammar.

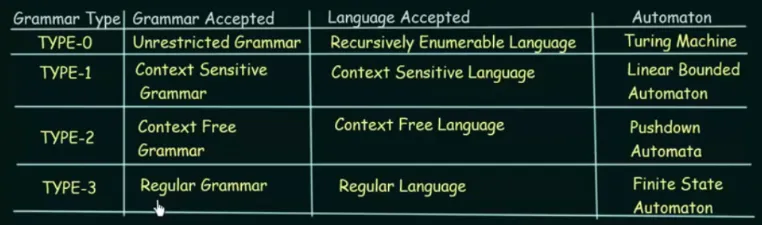
Source: https://youtu.be/WgEsPTAL55Q?si=4LOZ1qtkL1hunWmf&t=70

Every grammar generates its own language, which is recognized by a specific automaton.

Grammar

As explained in grammar, in general, a grammar is defined as quadruple: $G = (V, T, S, P)$.

With grammar $G_1 = (\{S, A, B\}, \{a, b\}, S, \{S \rightarrow AB, A \rightarrow a, B \rightarrow b\})$, we have three categories of symbol, $S$ (also known as the start symbol), $A$, and $B$. The category itself doesn't mean anything in language, the actual character that appears in the language are $a$ and $b$. The production rules describe that the start symbol $S$ can be replaced with $AB$. The $A$ and $B$ itself can be replaced by $a$ and $b$, respectively.

For example, starting from $S$
$S \rightarrow AB$ (by $S \rightarrow AB$)
$\rightarrow aB$ (by $A \rightarrow a$)
$\rightarrow ab$ (by $B \rightarrow b$)

The production rule of a general grammar is in the form of $A \rightarrow \alpha$, where $A$ is a non-terminal symbol, and $\alpha$ is a string of terminal or non-terminal symbol (formally $\alpha = \{V \cup T\}$). The production rule allows the transformation from non-terminal symbols to another non-terminal or terminal symbols, making it possible to expand the language recursively.

tip

The book also notate the production rule in the form of $(V \cup T)^+ \rightarrow (V \cup T)^*$. In other word, one or more terminal or non-terminal symbol can be transformed to zero or more (so includes empty string) terminal or non-terminal symbol.

For example, when the production rule generates another start symbol, such as $S \rightarrow SAB$, then, starting from $S$, we can produce $SAB$, then further apply the same production rule to obtain $SABAB$, and continue this process until we replace all non-terminal symbol to terminal symbol.

Example

The process of generating language from grammar is also known as derivation. The set of all language generated by some grammar is denoted as $L(G)$. The language generated by the previous grammar example, $L(G_1)$, consists of only a single string: $\{ab\}$.

Another example from the video:

Source: https://youtu.be/ejXgLRSIxsA?si=K8kIBdPOzhFgqsQW&t=573

This grammar has a recursive production rule. We can replace $A$ with $aA$, which mean we can potentially generate infinite amount of "a"'s. The language generated by this grammar creates a pattern $a^m b^n$, therefore the $L(G)$ is a set of string with that patterns.

Regular Grammar

Regular grammar is the grammar that describes regular language, which is the languages recognized by finite automaton like DFAs and NFAs.

Left & Right Grammar

The formal description of regular grammar is same as the general grammar, except the production rule follows either left or right types of grammar. With $A$, $B \in V$ and $x \in T$, right and left grammar is in the form:

• Right linear grammar: $A \rightarrow xB|x$, example $S \rightarrow abS|b$.
• Left linear grammar: $A \rightarrow Bx|x$, example $S \rightarrow Sbb|b$.

In right grammar, the production rule places non-terminal symbols on the right, while in a left grammar, it is the opposite.

Additionally,

info

The "|" in the notation $S \rightarrow A|a$ is a shorthand to describe two $S \rightarrow A$ and $S \rightarrow a$.

Context-Free Grammar

See the next topic.