Declarative & Functional Programming

Main Source:

• Declarative programming — Wikipedia
• Functional programming — Wikipedia

Declarative Programming

Declarative Programming is a programming paradigm that focuses on describing what the program should accomplish, rather than specifying how to achieve it. It is the opposite paradigm with the imperative programming.

The main characteristic of declarative programming is that it emphasizes the "what" rather than the "how" of a computation. This means that instead of writing step-by-step instructions for the computer to follow, we specify the desired outcome or the relationship between inputs and outputs.

Declarative programming works at higher level, it hides the implementation detail, making the code more readable and concise. On the other hand, imperative programming require explicit control flow. The system will decide how to execute the code based on the declaration, it doesn't have to be executed sequentially.

The abstraction of declarative programming makes it seem like magic, this can make it harder to predict how changes in the code will affect performance or behavior, especially if we are not familiar how the system works.

Source: https://steemit.com/programming/@nv-vn/getting-started-with-functional-programming

Functional Programming

Functional Programming (FP) is a programming paradigm (type of declarative programming) which treats computation as the evaluation of mathematical functions. Mathematical function is the framework of FP. In mathematics, a function is defined as a relation between a set of inputs (called arguments) and a set of possible outputs (called ranges), where each input is related to exactly one output.

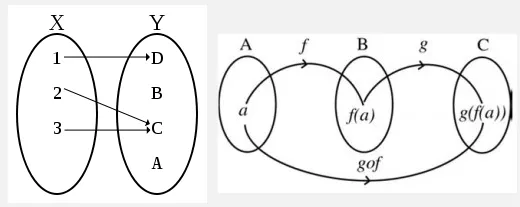
Source: https://web.cecs.pdx.edu/~antoy/Courses/CS250/slides/2b/Functions_2.html, https://danielpecos.com/2014/06/24/function-composition/ (function relation in math)

Characteristics of mathematical functions, which inherited into functional programming:

• Deterministic Mapping: For a given input, a mathematical function must produce a unique and deterministic output (same input should produce same output). The output is solely determined by the input.

• No Side Effects: A mathematical function should be pure, meaning it shouldn't have side effects. It shouldn't modify external state that cause the function to change its behavior.

  For example, a function f look like this:

  n = 2
  def f(x):
      result = x ** n
      n += 1
      return result

  It computes x to the power of n, then increments n, and finally returns the previous computation. This function has a side effect because its behavior modifies the variable n outside the function's scope. Even if it doesn't directly affect the function's output, we still consider it to produce a side effect. Side effects like this should be avoided in functional programming. A good principle is to not use global state or initial state at all.

• Referential Transparency: Referential transparency is a property of function that allows a function's output to be replaced by its equivalent output.

  Here's an example of referential transparency in Python programming language:

  # define function that takes two number and return the sum
  def add(x, y):
      return x + y
  
  result1 = add(3, 4)
  result2 = 3 + 4
  
  # Because the 'add' function is referentially transparent,
  # 'result1' and 'result2' will always be equal.

• Immutability: Immutability is a concept where once a variable (or data structure) is assigned a value, that value cannot be changed. Immutability is promoted in functional programming because it provides consistency; and again, it reduces potential side effects.

Lambda Calculus

Lambda Calculus is a concept of expressing computation in mathematical logic and computer science using functions.

Function is abstracted to anonymous function, they do not have name and is symbolized with the lambda symbol: $\lambda$. A function can take a parameter, it is placed in front of the lambda symbol. For example, a function with parameter $x$ is denoted as $\lambda x$.

After constructing a function, the next step is to apply an expression to the parameter, an expression or function body is denoted as $M$. Putting it all together, a function that takes a parameter $x$ and apply expression $M$ is denoted as $\lambda x.M$, where $.$ is just a symbol to separate the parameter from the body of the function.

Example

A function that takes some variable and return the variable incremented by 1, the lambda calculus notation for this is $\lambda x.x + 1$. When we apply this function with the argument of $3$, it would be written as $(\lambda x.x + 1) \space 3$, which is equal to $4$. The variable $x$ is bound to the argument $3$ during the function application.

That was just the basic concept of lambda calculus. Overall, it serves as the theoretical foundation for many concepts in functional programming languages. It provides a formal and mathematical framework for understanding functions, function application, and the manipulation of functions.

First-Class Citizen

In programming, an entity is called as a first-class citizen if it can be treated like other basic data types in the programming language. In functional programming, a function is treated as first-class citizen, it has several key characteristics:

• Assigned to Variables: We can assign a function to a variable, just like you would with a primitive data type.
• Stored in Data Structures: Functions can be stored in data structures, such as arrays.
• Passed as an Argument: A function can be passed as an argument to another function. In other word, a function can accept other functions as parameters.
• Returned from a Function: Functions can produce other functions as output.

In mathematics, the concept of first-class citizen is also known as a higher-order function.

info

In language like C, function is not considered as first-class citizen. However, it still allows us to pass function through argument, specifically using function pointer; that is, a pointer that holds an address of a function.

Language like Kotlin treat function as first-class citizen. We can, for example, define a function and assign it to a variable:

val add: (Int, Int) -> Int = { a, b -> a + b }

A variable named add has a data type of function that takes two Int values and returns an Int. Inside the function, we refer to the two Int arguments as a and b, and the output is produced by a + b.

Recursion

Functional languages depend on function, many features, such as iteration (e.g., for-loop) is not available. So, they must invent their "hacky" way to achieve such thing with function. Iteration can be achieved through recursion, which is a function that call itself until some condition is achieved. For example, we could make an illusion of loop in a function like:

def loop_for(n):
    if (n == 0):
        print("loop end")
    print("still looping...")
    loop_for(n - 1)

loop_for(3)

When we call the function with n = 3, the function will check if the input has reached zero or not. If not, it will print the "still looping..." and will call itself with its own input decremented by 1. This will be done until the n reached zero and the "loop end" will be printed.

Functional Programming Application

In the JavaScript programming language, a lambda expression (or arrow function) can be written as const addOne = (x) => x + 1. For example, calling addOne(5) will return 6.

As we can see, the expression (x) => x + 1 looks similar to the lambda calculus notation. It takes an argument x and returns the result of x + 1. The function is also assigned to the addOne variable (function as first-class citizen).

Another example of functional programming is the map function.

const numbers = [1, 2, 3, 4, 5];
numbers.map((x) => x * 2);

The map function is a commonly used function in functional programming that is used to transform each element in a collection with the provided function. Calling numbers.map() means we are going to transform each element in the numbers with the function given to the map function.

The function we provided to the map function is defined as a lambda expression, which takes x as parameter and return the x * 2. The result of the map function applied to the numbers array will be [2, 4, 6, 8, 10]

Here is another example from Wikipedia that compares imperative and functional programming approach to perform some operation to an array of numbers.

Source: https://en.wikipedia.org/wiki/Functional_programming#Imperative_vs._functional_programming

info

Modern programming languages often encompass different programming paradigms, combining one with another. Even though JavaScript supports for-loops, as typically found in imperative paradigms, it also supports functions as first-class citizens, which is the fundamental of functional programming.

tip

See also functional languages.